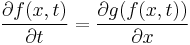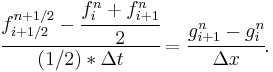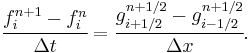Lax–Wendroff method

The Lax–Wendroff method, named after Peter Lax and Burton Wendroff, is a numerical method for the solution of hyperbolic partial differential equations, based on finite differences. It is second-order accurate in both space and time.

Suppose one has an equation of the following form:

$\frac{\partial f(x,t)}{\partial t}=\frac{\partial g(f(x,t))}{\partial x}\,$

where x and t are independent variables, and the initial state, ƒ(x, 0) is given.

The first step in the Lax–Wendroff method calculates values for ƒ(x, t) at half time steps, t_n + 1/2 and half grid points, x_i + 1/2. In the second step values at t_n + 1 are calculated using the data for t_n and t_n + 1/2.

First (Lax) step:

$\cfrac{f_{i%2B1/2}^{n%2B1/2} - \cfrac{f_i^n%2Bf_{i%2B1}^n}{2}}{(1/2) * \Delta t}=\cfrac{g_{i%2B1}^n - g_i^n}{\Delta x}.\,$

Second step:

$\cfrac{f_i^{n%2B1} - f_i^n}{\Delta t}=\cfrac{g_{i%2B1/2}^{n%2B1/2} - g_{i-1/2}^{n%2B1/2}}{\Delta x}.\,$

This method can be further applied to some systems of partial differential equations.

References

P.D Lax; B. Wendroff (1960). "Systems of conservation laws". Commun. Pure Appl Math. 13 (2): 217–237. doi:10.1002/cpa.3160130205.
Michael J. Thompson, An Introduction to Astrophysical Fluid Dynamics, Imperial College Press, London, 2006.
Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 20.1. Flux Conservative Initial Value Problems". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. p. 1040. ISBN 978-0-521-88068-8. http://apps.nrbook.com/empanel/index.html#pg=1040.

Numerical partial differential equations

Finite difference methods	Heat Equation and related: FTCS scheme · Crank–Nicolson method Hyperbolic: Lax–Friedrichs method · Lax–Wendroff method · MacCormack method · Upwind scheme · Other: Alternating direction implicit method · Finite-difference time-domain method

Finite volume methods	Godunov's scheme · High-resolution scheme · MUSCL scheme · AUSM · Riemann solver

Finite element methods	hp-FEM · Extended finite element method · Discontinuous Galerkin method · Spectral element method · Meshfree methods · Mortar methods

Other methods	Spectral method · Pseudospectral method · Method of lines · Multigrid methods · Collocation method · Level set method · Boundary element method · Immersed boundary method · Analytic element method · Particle-in-cell · Isogeometric analysis

Domain decomposition methods	Schur complement method · Fictitious domain method · Schwarz alternating method · Additive Schwarz method · Abstract additive Schwarz method · Neumann–Dirichlet method · Neumann–Neumann methods · Poincaré–Steklov operator · Balancing domain decomposition · BDDC · FETI · FETI-DP

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›